Sign Up to our MetaHub questions and Answers Engine to ask questions, answer members' questions, and connect with other teachers & members.
Login to our META-HUB questions & Answers Forum
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Please briefly explain why you feel this question should be reported.
Please briefly explain why you feel this answer should be reported.
Please briefly explain why you feel this user should be reported.
සම්භාවිතාව සොයන්න
Monty hall type එකේ ප්රශ්න ගැන පොඩ්ඩක් හොයල බලුවොත් idea එකක් ගන්න පුලුවන් වෙයි කියල හිතනවා.
Monty hall type එකේ ප්රශ්න ගැන පොඩ්ඩක් හොයල බලුවොත් idea එකක් ගන්න පුලුවන් වෙයි කියල හිතනවා.
See lessRational Numbers

See lessAny plans for provincial combined mathematics teacher training program for southern province planned?
We already had the program in the current series in the Southern Province. It was held in 2022. Did you miss it?
We already had the program in the current series in the Southern Province. It was held in 2022. Did you miss it?
See lessසරල රේඛාවක සමීකරණය
ගැටළුව තුල ඇති පින්තූරයේ සියල්ල නොපෙනෙන නිසා මෙය එවා ඇත
ගැටළුව තුල ඇති පින්තූරයේ සියල්ල නොපෙනෙන නිසා මෙය එවා ඇත
See lessගෝල ගැටුම්
සංස්ථිතික නියමවල ප්රයෝජනය පවතින්නේ යම් කාල පරාසයක් පුරා ඒවායේ යෙදීම තුළය. ඔබ එය ගැටුමක් සඳහා යොදන්නේ නම්, එසේ යොදනුයේ ගැටීමට මොහොතකට පෙර සහ ගැටුමට මොහොතකට පසු ප්රවේග පිළිබඳ තොරතුරු ලබා ගැනීම සඳහා ය. එබැවින්, එම තොරතුරු ලබා ගැනීමට වඩාත් සුදුසු ක්රමය නම් ගම්යතාවයේ හදිසි වෙනස්වීම් පාලනය කරන සමීකරණයRead more
සංස්ථිතික නියමවල ප්රයෝජනය පවතින්නේ යම් කාල පරාසයක් පුරා ඒවායේ යෙදීම තුළය. ඔබ එය ගැටුමක් සඳහා යොදන්නේ නම්, එසේ යොදනුයේ ගැටීමට මොහොතකට පෙර සහ ගැටුමට මොහොතකට පසු ප්රවේග පිළිබඳ තොරතුරු ලබා ගැනීම සඳහා ය.
එබැවින්, එම තොරතුරු ලබා ගැනීමට වඩාත් සුදුසු ක්රමය නම් ගම්යතාවයේ හදිසි වෙනස්වීම් පාලනය කරන සමීකරණය වන I=Δ(mv) යෙදීමයි.
The usefulness of conservation laws lies in their application over a period of time. If you are applying it for a collision, you will be applying it to get information on the velocities just before and just after the moment of impact.
Therefore, the more appropriate way to get that information is to apply I=Δ(mv) since it is the equation governing the sudden change in momentum.
~MetaHub Panel for Teachers’ Forum
See lessProblem solving
Here are some problem-solving books: 1. Mathematical Problem Solving by Alan Schoenfeld 2. Problem Solving Strategies by Arthur Engel 3. How to Solve It by George Polya 4. Problems and Solutions by G. L. Alexanderson, L. F. Klosinski, and L. C. Larson, (The William Lowell Putnam Mathematical CompetiRead more
Here are some problem-solving books:
1. Mathematical Problem Solving by Alan Schoenfeld
2. Problem Solving Strategies by Arthur Engel
3. How to Solve It by George Polya
4. Problems and Solutions by G. L. Alexanderson, L. F. Klosinski, and L. C. Larson, (The William Lowell Putnam Mathematical Competition1965–1984, Mathematical Association of America)
5. The Art and Craft of Problem Solving by Paul Zeitz
See lessසීමාව
The Sandwich Theorem can be applied even when the strict inequality is held in the hypothesis. For a more elaborate answer, please refer to the response given by us to your other question on limits. ~MetaHub Panel for Teachers’ Forum
The Sandwich Theorem can be applied even when the strict inequality is held in the hypothesis. For a more elaborate answer, please refer to the response given by us to your other question on limits.
~MetaHub Panel for Teachers’ Forum
See lessFactors

See lessProbability


See lessNumber Theory

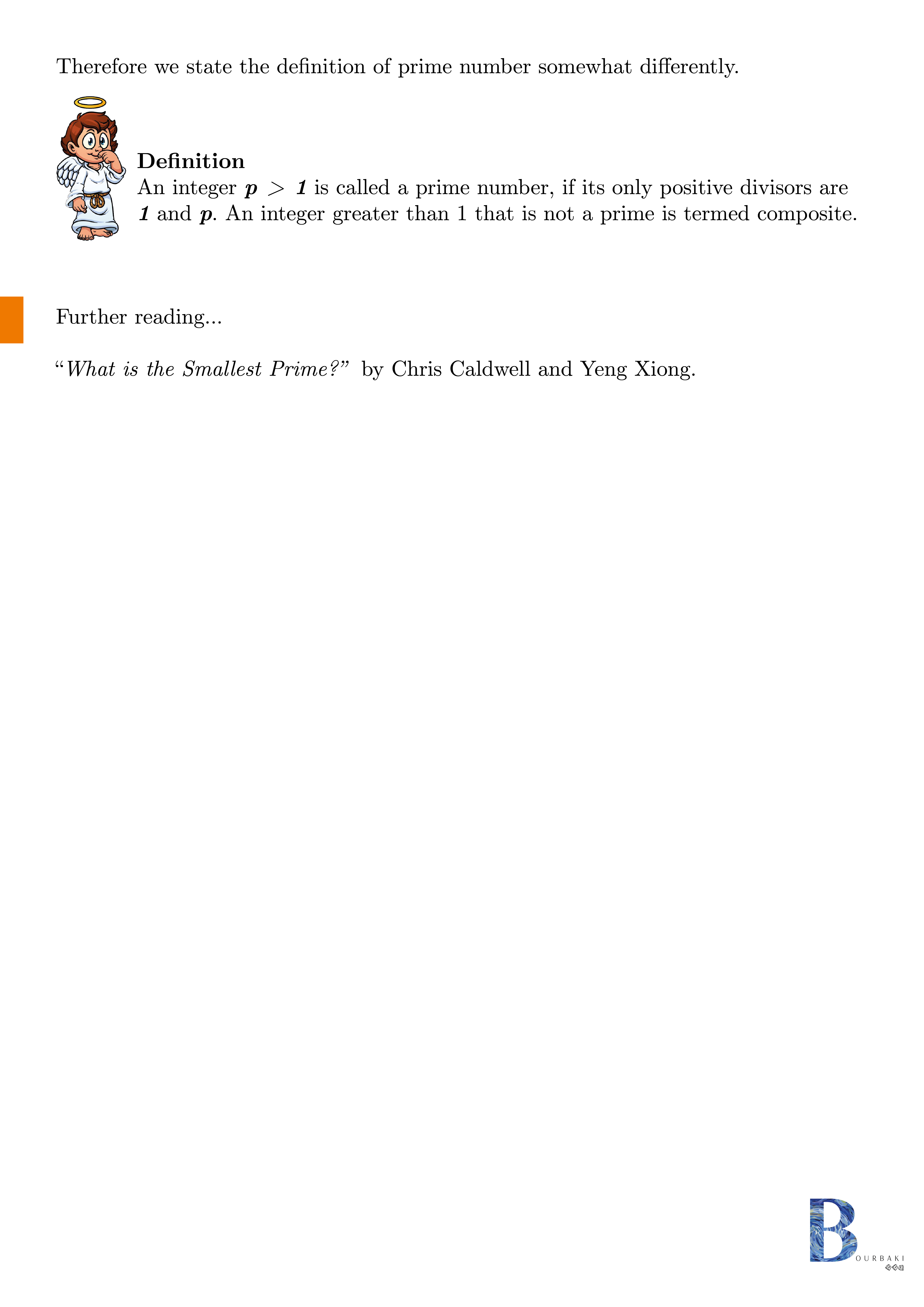
See less